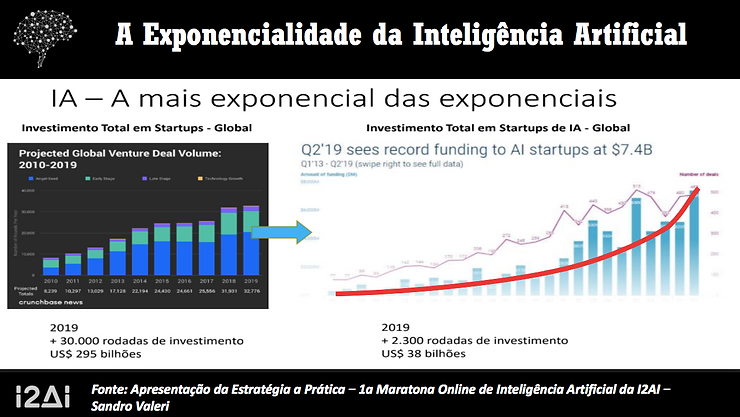
26/07/2023
O que é : Correlação espacial
O que é Correlação Espacial?
A correlação espacial é um conceito utilizado na área da estatística e geografia para analisar a relação entre os atributos de diferentes pontos em um determinado espaço geográfico. Essa técnica permite identificar padrões e tendências espaciais, revelando a existência de associações entre as variáveis estudadas.
Princípios
A correlação espacial é baseada em dois princípios fundamentais: a dependência espacial e a autocorrelação espacial. A dependência espacial ocorre quando os valores de uma variável em um local estão relacionados aos valores dos locais vizinhos. Já a autocorrelação espacial refere-se à semelhança dos valores de uma variável em diferentes locais.
Fatores Históricos
A correlação espacial tem suas raízes na geografia quantitativa e na análise espacial, que surgiram no final do século XIX. Com o avanço da tecnologia e o desenvolvimento de técnicas estatísticas, a correlação espacial tornou-se uma ferramenta poderosa para entender os padrões e processos espaciais.
Aplicações
A correlação espacial possui diversas aplicações em diferentes áreas, como geografia, ecologia, economia, saúde pública, entre outras. Alguns exemplos de aplicação incluem:
– Análise de padrões de distribuição de espécies em um ecossistema;
– Identificação de áreas de maior incidência de doenças;
– Estudo de padrões de migração populacional;
– Análise de padrões de distribuição de recursos naturais;
– Avaliação de impactos ambientais.
Importância
A correlação espacial é importante porque permite compreender as relações entre os fenômenos que ocorrem em diferentes locais. Essa análise pode fornecer insights valiosos para o planejamento urbano, gestão ambiental, tomada de decisões e desenvolvimento de políticas públicas.
Benefícios
A utilização da correlação espacial traz diversos benefícios, tais como:
1. Identificação de padrões espaciais: permite identificar agrupamentos, concentrações e dispersões de dados em um espaço geográfico;
2. Detecção de outliers espaciais: ajuda a identificar valores extremos que podem indicar problemas ou características especiais em determinadas áreas;
3. Análise de tendências: possibilita identificar tendências e prever possíveis cenários futuros;
4. Suporte à tomada de decisões: fornece informações relevantes para a tomada de decisões em diferentes áreas;
5. Melhoria no planejamento: auxilia no planejamento de ações e políticas públicas, considerando as características espaciais dos fenômenos estudados.
Desafios
A aplicação da correlação espacial também apresenta alguns desafios, como:
1. Definição de vizinhança: é necessário definir quais locais são considerados vizinhos, o que pode variar de acordo com o contexto e a escala de análise;
2. Escolha do método de análise: existem diferentes métodos estatísticos para calcular a correlação espacial, e a escolha do mais adequado depende das características dos dados e do objetivo da análise;
3. Interpretação dos resultados: a interpretação dos resultados da correlação espacial requer conhecimento e expertise na área de estudo, pois é necessário considerar o contexto e as particularidades do fenômeno analisado.
Exemplos
Dois exemplos de aplicação da correlação espacial são:
1. Estudo de criminalidade em uma cidade: a correlação espacial pode ser utilizada para identificar áreas de maior incidência de crimes e entender os fatores que contribuem para essa distribuição;
2. Análise de padrões de desmatamento: a correlação espacial pode ser aplicada para identificar áreas com maior taxa de desmatamento e entender os fatores socioeconômicos e ambientais que influenciam nesse processo.
Como funciona e para que serve?
A correlação espacial funciona através da análise estatística dos dados georreferenciados, levando em consideração a localização espacial de cada observação. Ela serve para identificar padrões, tendências e relações espaciais entre as variáveis estudadas, permitindo uma compreensão mais profunda dos fenômenos geográficos.
Tipos e Modelos
Existem diferentes tipos e modelos de correlação espacial, sendo alguns dos mais utilizados:
– Correlação de Pearson: avalia a relação linear entre duas variáveis;
– Índice de Moran: mede a autocorrelação espacial global;
– LISA (Local Indicators of Spatial Association): identifica padrões de autocorrelação espacial local;
– Geographically Weighted Regression (GWR): analisa a relação entre uma variável dependente e um conjunto de variáveis independentes, considerando a influência espacial.
Futuro
O futuro da correlação espacial está relacionado ao avanço das tecnologias de coleta e análise de dados georreferenciados, como o uso de sensores remotos, big data e inteligência artificial. Essas tecnologias permitirão uma análise mais detalhada e precisa dos padrões espaciais, contribuindo para o desenvolvimento de soluções mais eficientes e sustentáveis.
Tópico Adicional: Limitações
Apesar de ser uma técnica poderosa, a correlação espacial possui algumas limitações. Uma delas é a dependência da qualidade dos dados utilizados, pois informações imprecisas ou incompletas podem afetar a análise. Além disso, a correlação espacial não permite estabelecer relações de causa e efeito, apenas identifica associações entre as variáveis estudadas.
Tópico Adicional: Aplicações na Engenharia Civil
A correlação espacial também possui aplicações na engenharia civil, como no estudo de padrões de distribuição de infraestruturas, análise de riscos geotécnicos e planejamento urbano. Essa técnica pode auxiliar na identificação de áreas de maior necessidade de investimentos em infraestrutura, na avaliação de riscos de deslizamentos de terra e na otimização do uso do espaço urbano.
Resumo
A correlação espacial é uma técnica estatística utilizada para analisar a relação entre os atributos de diferentes pontos em um espaço geográfico. Ela permite identificar padrões, tendências e relações espaciais, sendo aplicada em diversas áreas, como geografia, ecologia, economia e saúde pública. A correlação espacial é importante para o planejamento urbano, gestão ambiental e tomada de decisões, trazendo benefícios como a identificação de padrões espaciais, detecção de outliers e suporte à tomada de decisões. No entanto, sua aplicação apresenta desafios, como a definição de vizinhança e a interpretação dos resultados. Existem diferentes tipos e modelos de correlação espacial, como a correlação de Pearson e o índice de Moran. O futuro da correlação espacial está relacionado ao avanço das tecnologias de coleta e análise de dados georreferenciados.